Frames of Reference - Galileo
Back to the main page/Back to the previous page

Jane stands still. See Jane stand still. So that Jane knows where she will stand, she establishes a reference frame for herself. Recognizing that she lives in a world with three spatial dimensions, she arbitrarily designates one dimension to extend to the right and calls it the x-direction. Holding with convention, she designates the other two coordinate axes the y-direction and the z-direction, and orients them according to the right hand rule. For convenience she locates the origin of her coordinate system at the point where she stands. Her coordinate system looks like the figure to the right. In this picture the z-axis is not shown, because we won't need a third dimension. If it were shown it would point directly out towards you.

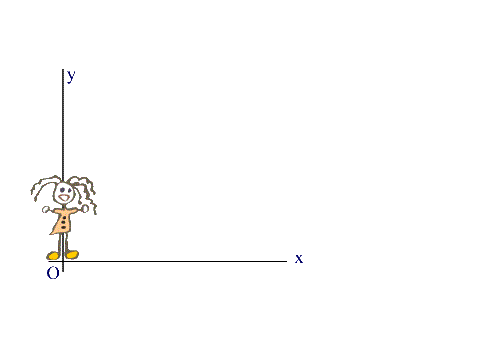See Dick ride past Jane on his little red wagon. Dick establishes his own reference frame and fixes it to his wagon. He rides past Jane at constant speed (which we will call v, for velocity), in the x-direction. To avoid confusion between his frame and Jane's, Dick labels his axes x' and y'. As Dick passes Jane they both start their stopwatches and mark the time when their origins coincide as time t = 0. At some later time t, Dick is a distance s from Jane, along the x-axis. There is no change in the relative positions between them in the y- (or z-) direction. Their separation is measured by the relation s = v t.

As an example, suppose Dick moves at 2 meters/second (v = 2 m/s). Then after 5 seconds Dick is 10 meters from Jane (s = v t, so 10 = 2 x 5). In the meantime, let's put Spot 28 meters from Jane, in the x-direction.  See Spot. How far is Spot from Dick? How far from Jane? Jane sees Spot at a fixed distance x (28 m) measured in her frame, and Dick sees spot at a distance x' in his frame. As time progresses Dick gets closer to Spot, but always the position of Spot as seen by Dick and Jane are related by x' = x - s, or equivalently x' = x - v t. If, for example, we take t to be 5 seconds, then Spot is at x' = 28 - 2 x 5 = 18 m from Dick. To complete the picture we can add, since we move along x only, that y = y' and, since both observers can use identical clocks, that t = t'. A diagram similar to the one on the right, but using the numbers from the example above can be found here. So what have we? Two simple notions you already knew: The first describes relative positions. If Jane stands at O, Dick is 10 meters east of her at O' and Spot stands 28 meters east of her, then Spot stands 18 meters east of Dick. The second describes relative motion. If Dick started from where Jane was (the origin O) and rode towards Spot at 2 meters per second, then after 5 seconds his distance from Spot compared to Jane's would be x' = 28 - (2 X 5) = 18 meters. It's all very simple, so why even mention it? Well, for two reasons: The first is because we build on this fundamental notion to describe all motion, and the second because it has historical significance, as the next paragraph explains.

I want to write these relationships out clearly, for they constitute two of the great ideas of science, and as we go along it will be part of our task to recognize and catalogue these great ideas. The first idea is that of Galileo, who, among his many contributions, brought quantitative measurement to science. His equations as used here are:

and constitute the famous Galilean transformation.

The second idea is represented in the x-y-coordinate system used in the figures, where the algebraic equations of Galileo are represented on the geometric diagram showing our coordinate system. Extended to the third spatial dimension (x, y, and z), we have Descartes' idea of analytic geometry, the merging of the two branches of mathematics, algebra and geometry.

Lets get back to our three actors: In the next scene Dick has caught Spot who now rides unsuspectingly along with Dick. Dick has restarted his trip past Jane and tosses poor Spot directly upwards just as he passes Jane.

See Dick throw Spot straight up in the air as they move along. What does Dick see? What does Jane see? What does Spot see?
Well, this sort of thing doesn't usually happen in the Dick and Jane stories you first learned to read with, but it makes a point. Dick, Jane and Spot each see different things, because they (and their reference frames) are moving relative to each other.

Dick sees Spot go up. Dick, in his frame fixed to the wagon, sees Spot move directly up and down, as shown by the black arrows. Both he and Spot are at rest with respect to the wagon, their reference frame. This may seem more plausible if you consider yourself in a similar situation in a train moving along a smooth railway at constant speed. You decide to throw a ball (or a cat, or ...) up and catch it as it comes down. You don't need to take the train's motion into account when you throw the ball - you throw it exactly as you would if you were standing on the ground. In your reference frame you are at rest. The key words here are "constant speed". If there is acceleration (as Spot will find out), things get involved. Jane sees Spot arc through the air. The combined motion resulting from the wagon moving along the x-direction and Spot moving (relative to the wagon) along the y-direction is seen by Jane as the parabolic curve shown by the blue dots.  Spot is confused. Actually, Spot may be aware of his predicament, as he has no good reference frame to call upon. However, consider Spot's favorite flea Alex, who finds himself at rest of the back of Spot. In spite of this anchor to what is for Alex a fixed frame, he sees Dick and Jane moving in a way not explainable using the equations derived under conditions of uniform motion. Alex's frame is not moving with constant speed, but rather is accelerating as Spot sails through the air under the influence of gravity. More about this later.

The combination of these two motions was observed by Galileo as he methodically applied what has come to be the scientific method to his experiments with falling bodies. His measurements led to the relation describing the curved path Spot is forced to take as a result of Dick's experiment. Unlike the motion of Dick, Spot comes under the influence of gravity's constant downward acceleration. The result of Galileo's work is summarized in his equations of motion. His equations came from repeated experiments wherein he rolled balls down smooth inclines (rather than by dropping them in order to slow down the effects of gravity). Timing the events with a water clock of his own invention his measurements led to the equations, which are valid for a body experiencing what he called naturally accelerated motion. They are the two equations shown below.

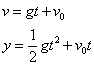Here Galileo describes the velocity (v) and position (y) of a body falling under the acceleration provided by gravity (g) as time (t) proceeds. The term vo accommodates the possibility that the object may have had an initial velocity (vo ) when the experiment first started. If the second equation here is combined with the the equation s = v t (with s replaced by x in keeping with our x- and y- coordinates), we have the equation (worked out here) representing the dotted trajectory of our friend Spot, as seen by Jane. At this juncture you should view these equations as a lesson in history rather than mathematics - the point being that motions observed from different reference frames can be reconciled by applying the relationships found by Galileo.

Galileo's equations of naturally accelerated motion were empirical - the result of many experiments and the analysis of the resulting data. He was not able to  extend his experiments to a more universal theory of motion. That was meant to be the task of Isaac Newton, as we will see in what follows.
Go to the top
Go to the page on Newton's frames of reference