The Lorentz-FitzGerald Contraction

Suppose a flash of light goes off at the origin of a coordinate system. The light will propagate outward in the shape of a sphere, with the wavefront moving at the velocity of light, which everybody calls c. In this coordinate system the equation for the wavefront is

To see this, recall that the equation for a sphere is x² + y² + z² = r² , where r is the radius of the sphere. Since the wavefront moves outward at velocity c, its distance from the center (the origin) at any time t must be r = ct.  Now suppose another observer is traveling at velocity v along the x-axis, and his origin coincides with the at-rest coordinate system above just as the flash of light goes off.  In his coordinate system the equation for the wavefront is

,

where the moving coordinate system is marked with primes ('), to distinguish it from the fixed frame. Notice that we do not assume that t = t', but we do assume that c is the same for both observers, in accordance with the results of the Michelson-Morley experiment. The Galilean transformation requires that 

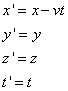
as we saw before (the z-coordinate is added in keeping with our 3-dimensional approach). Substitute these into the primed equation above and the result is

which is clearly not the first equation for the sphere in the unprimed system. If we require c to be unchanged between systems, the Galilean transformation fails! But wait: We know it works for most situations (i.e. low velocities), so we need to try to fix the Galilean transformations in such a way that the constancy of c is preserved, but so are the Galilean transformations for low velocities. Clearly the problem lies with the equation t = t'. The earlier discussion on simultaneity pointed this out. We try a different equation t = t' + a x, where a is constant term we need to find. Why this particular equation? Well, it's quite a simple modification, and we should try the simple fixes before the more complex ones and, in hindsight, it happens to work! What follows is some fairly simple algebra leading to the "relativistic factor" g. This factor becomes the modifier of length, time and mass as viewed from moving coordinate systems. If you want to follow the math through, references 2 and 3, as well as many other introductory level physics texts, provide the details.