Statistical Mechanics

Statistical Mechanics - A random walk through physics

What is temperature? We use the term all the time, and we know what it means - how hot something is. What does hot mean? Something that's at a high temperature. How about heat? That's what you get from something that's hot - i.e. at a high temperature. See the problem? Although we can work with heat, hot (or cold) and temperature it's hard to define them without the cyclic result above. There's another way that involves, strangely enough, statistics.

First, a brief problem in probability - the classic "random walk" problem: A drunk stands at a lamp pole and decides to walk along the sidewalk. The sidewalk is straight but not necessarily level and the drunk is unable to control which way he steps (except that he manages to keep on the sidewalk, avoiding the gutter). Question: Assuming that he takes steps of equal length with equal probability that the steps are right or left, where will he be after a total of N steps?

Call the length of each step µ and the probability of a step to the right p. Then the probability of a step to the left is 1 - p, which we can call q. In general, because the sidewalk may not be level, p ! q - i.e. he may be more likely to walk down hill rather than up. Choose the origin to be at x = 0. The situation then looks like that in the diagram. Stating the question differently, as each step is of length µ , the man must be at a position x = m µ after N steps, m being an integer. If m is zero he ends up where he started; if positive to the right, and if negative to the left. Clearly m lies between -N and +N (or may be at either extreme). Our task is to find the probability P(m) that he is at x = m µ after N steps (e.g. what the chance is that x = 0, or x = 3 µ or some other stated position).

Call n_r the number of steps taken to the right and n_l the number of steps to the left. then N = n_r + n_l . Also, m = n_r - n_l since m was chosen to be positive for steps to the right. Using these two relations provides m = 2 n_r - N which indicates that m is even or odd as N is. As each step is, because of our friend's condition, independent of the earlier ones, the probability of a particular sequence of steps is just the product of the individual probabilities. As a familiar example, flipping a coin once gives equal probability (50%, or 1/2) of heads or tail and flipping it again provides the same equal chance for heads or tails on the second try. However the probability of both tosses yielding a particular result (both heads, say) is only 25%, or 1/4. The outcome of the coin toss can be H-H, T-T, H-T or T-H. the probability of any particular one of these outcomes occurring is the product of the individual probabilities - 1/2 * 1/2 = 1/4. A particular outcome for 3 tosses would be 1/2 * 1/2 * 1/2 = (1/2)³ = 1/8 and for n tosses (1/2)ⁿ. In our random walk case the probability is p for right steps and q for left steps, so for n_r steps to the right and n_l steps to the left the probability of a particular outcome is

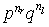
Of course, many of the outcomes may have the same end result - there are many sets of steps that will get the drunk back to the lamp pole, and in the case of the coins the H-T and T-H outcomes are distinct only if they are identifiable - say one coin is painted red and the other green - otherwise they can be considered to represent the same outcome. In this case there are only 3 possible outcomes H-H (25%, or 1/4); T-T (25%, or 1/4); and H-T (50% or 1/2). In fact, the number of distinct outcomes is

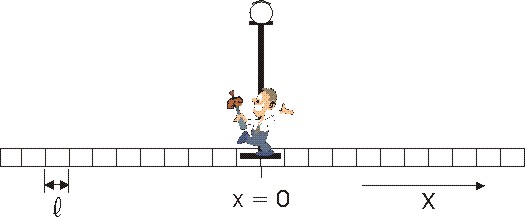You can test this on the coin toss: There N = 2, n_r the number of heads and n_l the number of tails. For 2 heads and 0 tails the number of possible outcomes are 2!/2! * 0! = 1; for 1 head and 1 tail 2!/1!*1! = 2. You may be better convinced if you try three or four coins. Just note that the coin toss is the same as the random walk if the walk uses equal probabilities for right and left steps (and the coins are "fair"). Another look at the reasoning behind this result can be found here.

So - when the number of distinct outcomes is included, P(n_r) - the probability of taking n_r steps to the right out of a total of N steps (and so n_l steps to the left) is given by

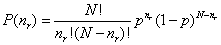
where I have used n_l = N - n_r and q = 1 - p.

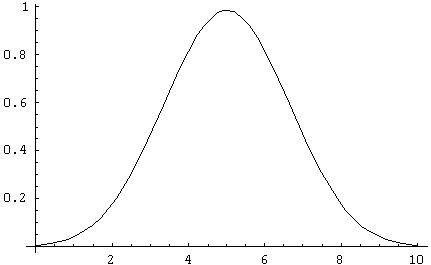
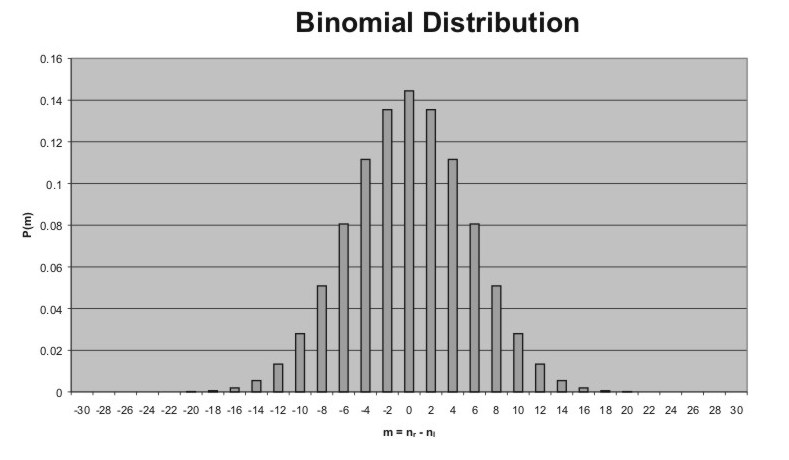
The probability P(n_r) is called the binomial probability distribution. The characteristics of a series of events governed by this distribution (like our random walk) are displayed as the familiar pattern shown to the right. There our drunk has taken 30 steps with equal likelihood of them being left or right. The probabilities for -30 to +30 steps net displacement from 0 are shown, using the relations N = n_r + n_l and m = n_r - n_l . Again recall that m must be even if N is even. As you would expect for a level sidewalk our friend will most likely make no progress at all, but rather end back where he started. This is not unexpected - you may have guessed the outcome. You also might guess that the average number of steps to the right is just N*p and to the left is N*q. (You can check this by noting that for 30 steps on level ground N*p = 30*(1/2) = 15 , and N*q = 15, leaving on average our drunk back at the lamp post. As a further check you can see that these values provide the required result

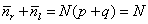
where the bars over n_r and n_l indicate their average values N*p and N*q as mentioned above. In terms of the displacement m, since m = n_r - n_l the average displacement is given by

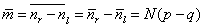
which for p = q gives the net displacement of zero shown.

We need to have one more piece of information: How broad is the distribution of values about the average (the so-called standard deviation), or even more revealing, how does this deviation from the average depend on the number of steps - i.e. the relative deviation? The answer involves more math than we can afford here (see Ref #6), but the simple result is that the relative deviation, i.e. the ratio of the deviation to the average number of steps, is proportional to the reciprocal square root of N :

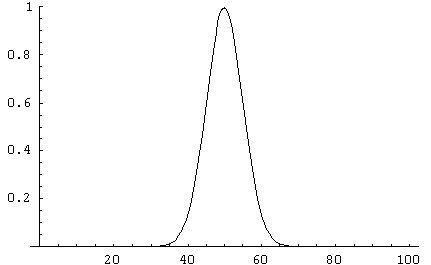
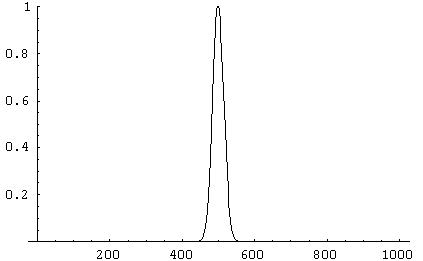
Thus as N (and so n_r ) gets larger the relative spread in values about the average gets smaller. Some graphs may make this clearer: Below are distributions for N = 10, 100 and 1,000. The sharp decrease in the relative widths of the curves is immediately obvious.

The sharpness of the distribution is the key. As the number of events gets large the variation from the average outcome gets (significantly) less. This is the statisticians dream - with large enough samples the chances of predicting the outcome increase. In this sense the physicist is in an admirable position - the behavior of gas molecules in a container involve values of N on the order of 10²³!

Here's a simple example: A container (perhaps of total volume 1 liter) is partitioned into two equal parts. On the left side of the partition there are 4 gas molecules, on the right side none. The partition is removed and the system (the container and the molecules) is allowed to reach a final state of equilibrium. Where are the 4 molecules? To answer this we apply the lessons of the random walk (or, for such a small number of possible arrangements, simply count the possibilities). Each molecule has an equal chance of being on the right or on the left; p = q = 1/2. Then for 4 molecules there is a 1/16 chance none will be on the right. The probabilities for 0, 1, 2, 3 or 4 molecules being found on the right side are shown to the left. If instead there were 100 molecules the chance of there being none on the right becomes 7.9 x 10^-31 - a fantastically small number! The molecules are always moving around and are equally likely to be on the right or the left at any given time. If you took a snapshot of the arrangements every second you would have to wait, on average, 4 x 10²² years (10 billion times the age of the universe) to get a picture of them all bunched on the same side. Conversely, the probability of the molecules being evenly distributed between the two sides is 0.08 - fairly likely by comparison. This value obviously drops rapidly on either side of the average (as in the curves above).	Number on the right side	Probability
	0	1/16
	1	1/4
	2	3/8
	3	1/4
	4	1/16

This is just counting - how does it tie in with science? The example above depended on each possible state of the molecules (i.e. right side or left side) being equally accessible. If there were many partitions rather than just 2 the situation should still hold - no position is more likely than any other. Further, if a constraint on the number of available states of a system is released (i.e. more states become available, as when the partition above is removed), these newly available positions will quickly be populated. Why? Because it is highly unlikely that they won't. The final equilibrium situation will thus be the one in which the number of states is maximum. This does not forbid variations from this equilibrium condition, just as flipping 100 coins will not always (or usually) result in exactly 50 heads and 50 tails., but the variations about equilibrium will small and, when the system does find itself in a non-equilibrium state it will quickly retreat from it.

Suppose we replace the available cubby holes with some other available state - say the energy of a molecule of the gas, or with a combination of characterizations of the molecules that make up their energy, such as position, momentum and perhaps rotation (if they are complex gas molecules such as carbon dioxide). Now there are hugely more available states for the system, but they still should be occupied an a way that is most probable and, as in the simple container of gas described above, the most likely state is a uniform distribution. More so, it would be fantastically unlikely that the system would stray very far from this equilibrium condition at all. As a simple measure of the number of available states, consider a container of gas with N molecules. The energy of this system is E = K + U + E_internal , where K and U are the system's kinetic and potential energies and E_internal represents the internal energy of the molecules, due perhaps to their complex structure. In the case of an ideal gas (where the molecules are considered to be points) the internal energy would be zero. It follows then that the total number of states of a system S = V^N F(E), where F(E) is the total of all the possible combinations of momentum and position for all the molecules - i.e. the available energy states. If N is of the order of Avogadro's number (10²³) the number of available states is indeed large.