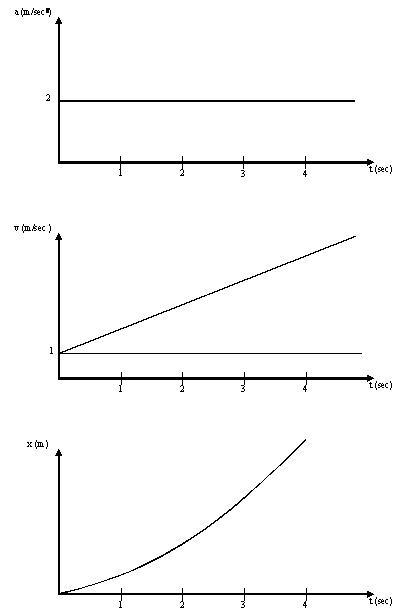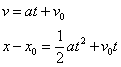The Copernican Revolution
Of all the motions there were, motions of
the heavenly bodies most occupied the thoughts of ancient thinkers. The Pythagoreans
put Earth at the center of the universe and the planets (including our Sun and
Moon) on spheres turning around it. Variations of this model were proposed (most
notably by Aristarchus
in about 200 BC), but the matter was essentially settled by Plato
when he posed the problem of finding the best combinations of circular orbits to
explain the motions of the planets. The most successful attempt was by Claudius
Ptolemy in about 100 AD. Using the idea of epicycles proposed by Hipparchus
over 200 years earlier, he created a complex model (the Ptolemaic
system) that could predict the motions fairly accurately - Plato's problem
had been solved. The Ptolemaic system was accurate enough (although modified -
and made more complex - over time) to stand for fifteen centuries until, looking
for a simpler way, Nicolaus
Copernicus moved the center of the World to the Sun.
From Impetus to Inertia
He was a major contributor to the Copernican
Revolution, but a greater contribution of Galileo Galilei is his work on the motion
of falling bodies. He was born in Pisa, Italy in the same year as
Shakespeare, on the day that Michelangelo died: 1564. He died in 1642, the year
Newton was born. His work "Discourses on Two New Sciences" was
published in 1638 while he was under house arrest for his support of the
Copernican view of planetary motion. This work was much more that an explanation
of the mechanics of how objects moved, it was the beginnings of modern science.
For the first time a theory was valid only when verified by experiment, and the
scientific method was established. Here is a brief description of his "new
science" - the presentation is streamlined, but the ideas are Galileo's.
Uniform Motion: Wherein equal distances
are covered in equal times.
Uniformly Accelerated Motion: Wherein the
motion gains equal increments of speed in equal time intervals.
These relations he acquired through
experimentation and reduction of data - what we call the experimental method
began here.
The connections between distance,
velocity and acceleration can be seen directly when presented in graphical form:
Here, a graph of
acceleration with a constant value of 2 meters/sec2 is shown -
it's just a straight line of value 2, which never changes. This is a
particularly important case: First, it's simple; second it is the same
situation we find all the time when something falls under the influence of
gravity. (If it were the case of Earth's gravity, the acceleration would
be equal to 9.8 meters/sec2.)
OK: If you accelerate (from rest)
at 2 meters/sec2 for say, 1 second, how fast are you going? You
should be able to figure it out - the answer is 2 meters/sec. After 2
seconds your speed will be 4 meters/sec., after 3 seconds it will be 6
meters/sec., etc. A graph of this is shown below. For completeness I have
added a constant starting velocity to the motion. That is, rather than
starting from rest I start at an initial speed of 1 m/s. Of course, this
starting speed just pushes the curve upward by 1 m/s everywhere along the
curve.
One more step: From the velocity we
should be able to find the distance covered. This is shown in the third
graph. In the first second we move at 1 m/s due to our initial velocity; 1
m/s for 1 second gets us to the 1 meter point. We must add to this the
distance traveled due to the acceleration. The velocity changes during the
first second, but our average velocity (due to the acceleration
only - we already have counted our starting velocity) is 1 m/s (We start
at 0 m/s and end at 2 m/s. The average is (2 + 0)/2 = 1). The distance
covered after 1 second is then 2 meters (1 meter due to our initial
velocity and 1 due to the acceleration). Keep doing this and you get the
curve shown. A chart of values is shown below.
| Distance
covered due to a constant acceleration of 2 m/s2 and an
initial velocity of 1 m/s. |
| t (seconds) |
1 |
2 |
3 |
4 |
| x (due to v0) |
1 |
2 |
3 |
4 |
| x (due to a) |
1 |
4 |
9 |
16 |
| x (total) |
2 |
6 |
12 |
20 |
Galileo found this out
through experimentation - rolling balls down an inclined plane. Newton
derived the same from basic principles - his laws of motion.
|
 |
Before leaving this matter, there's one
important observation to make. If you followed the calculations above you
arrived at the results shown, but it took some careful reasoning and an
understanding of how things move. Put that aside now and look at a purely
geometrical problem related to the curves: Start with the acceleration curve and
calculate the area under the curve from time zero until time 1 second. It's easy
to see that the area is (height times width) 2 x 1 = 2. After 2 seconds the
total area is 2 x 2 = 4. After 3 seconds the area is 6, then 8 then 10. These
numbers are exactly the velocity achieved because of the acceleration! of
course, when you multiply length times height you must also multiply the units,
which are m/second2 times seconds = m/second, the units for velocity.
Conclusion: the area under the acceleration curve is a measure of the velocity.
As an exercise you should calculate the area under the velocity curve. Guess
what - it provides the values for x, the displacement. Geometry solves problems
in physics! Finally, if you remember what the slope of a line is, you can see
that the slope of the velocity curve is exactly 2, the value of acceleration.
The language of physics is mathematics.
Basic Ideas about Motion
We need to be able to describe the motion
of things (for obvious reasons). To be coherent in a discussion of motion, we
first must agree on a common vocabulary, so I show here a glossary of terms we
will use:
Speed:
How fast our object is moving.
Velocity: How fast (or more
formally, the rate at which) our object is moving, and the direction in
which it is moving.
(Already, we have come upon an important distinction - speed
can be described by a number, say 20 m/s, but for velocity we require more.
We take the velocity of our object to be its speed combined
with the direction of its motion. This distinction is generalized into the
mathematical ideas of scalars and vectors, which we define next).
Scalars:
A scalar is something whose measure is defined
by its magnitude. Examples are speed (how fast), temperature (how hot), length
(how long), and many more. (Think of a few).
Vectors:
Vectors require direction as well as magnitude
to describe their measure. Examples are velocity (speed, and the direction of
the motion; 20 m/s to the northeast), Force (how hard you push, and in what
direction - to convince yourself that force is a vector rather than a scalar,
try pushing on something without pushing in a particular direction). There are many
more. (Again, try to think of some).
Now we can get back to motion:
Acceleration: The rate at which velocity changes. Now we may be getting
into new territory. Not that you haven't heard of acceleration, but have you really thought
about it. You drive along at 40 miles per hour. Your speed is constant and
you are on a straight section of road , so your direction and speed, and so your velocity
does not change. Your acceleration is zero, right? Sure it is. Now you step on
the gas, and you accelerate - you go faster. How much faster? If for every
second you keep accelerating your velocity increases by, say, 2 miles per hour,
your acceleration is 2 miles per hour per second. Using more consistent
(if less familiar) units, lets say you accelerate at a rate of 2 meters per
second every second. Your acceleration is 2 m/s per sec, or 2 m/s2.
Position:
Where our object is, relative to some reference frame. The reference frame
defines the origin of our coordinate system, from which all measurements are
made.
With these definitions we can describe
the motion of an object. By an object I mean a simple particle, consisting of a
single point in space. It can also be a point representing an object whose size
makes its extent negligible compared to the rest of the system under
consideration. For example, a baseball is essentially a point compared to a
baseball stadium, as is the earth compared to the solar system.
Newton's theory of motion
In the "Principia"
(Mathematical Principles of Natural Philosophy), Newton's monumental work
published in 1687, he presented the motions of planets and things terrestrial in
a form both compact and comprehensive. He generalized the work of Galileo into
two laws, added a third law, and explained the law by which the gravitational
force between massive objects work. Because of this the workings of the world
became thought of as a giant clockwork which, once started, could be predicted
from that point forward by a simple application of his laws of motion. Few
others in the history of mankind contributed more to its direction. In
formulating his laws he first defined some basic quantities:
Mass:
"The quantity of matter is the measure of the same, arising from its
density and bulk conjointly."
In modern terms, the mass of an object is its
density times its volume (m = D
V).
Momentum: "The
quantity of motion is the measure of the same, arising from the velocity and
quantity of matter conjointly."
In modern terms, the quantity of motion is called
momentum, and we write momentum as the product of mass and velocity (p = m
v).
Force: "An
impressed force is an action exerted upon a body, in order to change its
state, either of rest, or of uniform motion in a right (we would say
straight) line."
Thus the tendency of objects to maintain their state of
motion (inertia) is overcome by the application of a force.
He then postulates his three laws of
motion:
The law of inertia (Newton's first
law):
"Every body continues in its state of rest, or of
uniform motion in a right line, unless it is compelled to change that state
by forces impressed upon it."
The means by which an object's motion
is changed (Newton's second law):
"The change of motion is proportional to the motive
force impressed; and is made in the direction of the right line in which
that force is impressed."
The law of action and reaction
(Newton's third law):
"To every action there is always opposed an equal
reaction: or, the mutual actions of two bodies upon each other are always
equal, and directed to contrary parts."
In terms of momentum (the quantity of
motion) we can say that a force F applied to an object (of some mass m)
over some time interval )t,
will change the object's momentum. As an equation, F
)t
= )(m
v). If this change in momentum
involves a change in the velocity of an object of fixed mass (the usual case of,
for example, someone throwing a baseball), we can divide our equation by )t
and have F = m )v/)t.
Since )v/)t,
the change of an object's velocity over a time interval, is just that
object's acceleration, we have the common expression of Newton's second law, F
= m a..
These three laws form the basis for the
entire subject we call mechanics today. Except for corrections pointed out by
Einstein, they are all we need.
To see how his law of gravitation is
formulated, we need to look at what is called "uniform circular
motion": Think of a ball going around on the end of a string or, as Newton
did, the Moon going around the Earth. If the motion is uniform (i.e. at constant
speed as it goes around) it nonetheless must be accelerating because its direction
of motion is changing, even if its magnitude is not. It is accelerating without
changing speed - how can that be? It must be accelerating at right angles to its
direction of motion (think about it)! Conclusion: If an object moves with
uniform motion it must accelerate towards the center of its circular orbit. What
is the magnitude of this central (centripetal) acceleration? Well, that takes a
bit of mathematics (click here if you want to see how it is done), resulting in
the expression ac = v2/r. In order for this
acceleration to occur (according to Newton's 2nd law), there must be a force.
thus, if an object of some mass (m) is to move in a circular path, a
center-seeking force of magnitude Fc = m v2/r must
be acting on it. This is the famous centripetal force you may have heard of. In
the case of the ball and string it is the tension in the string that provides
the force; for the Earth and Moon, gravity does the job. Just how gravity
provides the necessary force Newton deduced from Kepler's laws combined with his
second law, along with the assumption that Nature didn't care if the forces were
between Sun and planet (Kepler), ball and string (on Earth), or Earth and Moon
(Newton's quest). The result is Newton's universal law of gravitation, written
as
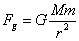 .
.
Here the left side represents the force
due to gravity - the mutual attraction of any two objects of masses m and
M. The right side states that this force is proportional to the product of
the two masses (m and M) and inversely proportional to the square
of the distances between them. With this single equation the motions of
the heavenly bodies become known - Plato's problem is solved (without the
circles). How accurate is this universal law? Well, we know that on
24 July in the year 3991 there will be a total eclipse of the sun beginning at
22:20 O’clock (Universal Time), and it will last 7 minutes, 18 seconds (we
also know just where on Earth one should be to see it). The power of Newton’s
laws should be obvious.
Conservation of Momentum
Newton spoke of mass as the quantity of
matter, and momentum as the quantity of motion. Both these quantities lead to
important results. We look first at momentum:
Typically the letter p is used to
represent the momentum of an object. We write p = m v. (The
momentum of an object is, as defined by Newton, its mass times its velocity).
Starting from Newton's second law we can write
F = ma = m )v/)t,
since acceleration a is just a measure of how velocity changes with time. As
was implied in the page on Newton's laws, this form of the second law assumes
the mass remains constant. The more general statement of the second law moves
the mass back along side the velocity, providing F = )(m
v)/)t,
or F = )p/)t.
This form reduces to the familiar form F = m a in the case of
constant mass, but allows for a time varying mass if the occasion demands (as,
for example, in the case of the launch of the space shuttle, where the fuel
outweighs the shuttle).
Suppose two objects (we like to call them
particles) collide head on, one coming in
from the left, the other from the right. According to Newton's third law, the
force that the first particle exerts on the second is equal and opposite to the
force the second exerts on the first. As an equation, we write F1-2
= - F2-1 where the subscript 1-2 means the force Particle #1
exerts on #2, and 2-1 the force #2 exerts on #1. In other words, the forces are
equal and opposite. Using Newton's second law we can rewrite this as )p2/)t
= - )p1/)t.
This simply states that when the force of #1 is felt by #2 the result is a
change in #2's momentum, and likewise in the other direction. If the right-hand
term is moved to the left we have )p2/)t
+ )p1/)t
= 0, which says that the total change in momentum of both particles is zero.
How can the total change be zero? Only if the total momentum (p1
+ p2 ) remain constant. Note that either one can change,
but the total momentum remains constant. This is the law of conservation
of momentum. It is the first of the great conservation laws that provide us with
powerful concepts for our study of physical phenomenon. Here's an example of how
it works:
In the game of billiards the cue ball
strikes an (at rest) object ball, and then stops. How fast does the object ball
move after the collision? Answer: Just as fast as the cue ball was moving. Why?
Conservation of momentum.
Conservation of Energy
What is energy? Everyone knows what
energy is - we use it all the time, but how is it defined? Write down your
definition before you read further. Chances are you had a difficult time
defining energy. Here's a definition from Webster's New World Dictionary, Third
College Edition: "the capacity for doing work" (along with many other,
non-scientific definitions). OK, then what is work? "the means by which
energy is transferred" (again, along with many other definitions). Here's
how we define one kind of energy:
We start with a definition of work: Work
is the product of the force applied to an object times the displacement of the
object due to the force. We are careful to count only the force which is applied
in the direction of the motion. Here's an example: You push a box along the
floor, pushing exactly in the direction the box moves. If your force is 10
Newtons and the box moves 3 meters you have done 30 Newton-meters of work. (A
Newton in the SI system of units is equal to about 0.225 pounds; a Newton-meter
is more usually called a Joule). Now suppose you push the same box the same
distance, but this time you push downward at an angle of, say 600 from
the floor. Now some of your effort is trying to push the box into the
floor. To get the same 10 Newtons of force in the direction the box moves you
have to exert a total force of 20 Newtons. You do the same work - 10N times 3 m,
but you may be a bit more tired if you move the box this way.
So: Work = Force X distance (remembering
the its the force in the direction of movement that counts). Suppose a force F
causes a movement )x.
The work done if F
)x.
Since F = m a, it follows that
Since F = m a, it follows that
F
)x
= m a )x.
Remember Galileo's equations of
motion? I reproduce them here for convenience (I've changed y to x and x to x -
x0 to make things a bit more general):
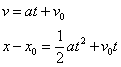
A little algebra should convince you that,
if you eliminate time from these two equations you arrive at an expression
relating velocity, position and acceleration. It turns out to be (you should
verify the result for yourself)
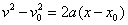 .
.
Now x - x0 is just )x,
and, if I solve this equation for
a and put the result into the equation for work above (F
)x
= m a )x),
the result is
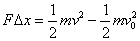 .
.
F
)x
is the work done on the mass
m. The expression on the right is
defined to be the kinetic energy of the mass m. (Actually the right hand
side represents the change in kinetic energy - its initial kinetic energy was
1/2 m v02 and its final kinetic energy was 1/2 m v2.)
So, energy is a concept. It is an
idea useful in describing what happens to something when work is done on it. The
change in kinetic energy of an object is a measure of the work done on it. We
call kinetic energy "energy of motion" (for obvious reasons).
Remember when we multiplied F by )t
and eventually arrived at
conservation of momentum? It turns out that multiplying F by )x
provides another conservation
law, conservation of energy. In its most general form it states that the total
energy in the universe is conserved. We may change its form from one kind of
energy to another, but the total remains constant. Perhaps the most remarkable
thing about this law is that it deals with our invented concept of
energy. It is actually a convenient bookkeeping scheme upon which the very
foundations of physics are built.
I speak of conservation of energy, but
its easy to find a problem with what I have said so far: Think of two identical
pucks on an air table coming toward each other at some speed v. They each have
kinetic energy 1/2 m v2. After they collide they are each moving away
from each other and it's easy to show that they will each have kinetic energy 1/2 m v2
as before - energy is conserved. But for a brief time both pucks have stopped,
at the instant they collide. Where was the energy then? Well, as they collide
the two pucks distort somewhat and then regain their original shape. In doing so
the pucks push away from each other, thereby getting their energy back. We say
that there is energy stored in the distorted pucks (as if the pucks were made of
tiny springs that compress and then release). This form of stored energy is
named "potential energy". An example in a different context may be
useful: Suppose you have a weight (give it mass m) that you lift a height
h above the floor. How do you do his? You apply a force that overcomes
Earth's gravity and exert that force over a distance h - you do work!
This work moves the weight upwards. Once at the height h you can hold it
there (or put it on a shelf) and, whenever you want, let it fall to the ground.
As it falls, it converts that stored potential energy into energy of motion -
kinetic energy. So it is the combined energy that is conserved - kinetic plus
potential (in this case gravitational potential). Carry the process one step
further: On the floor under the weight place a coiled spring. The weight falls,
lands on and compresses the spring and then rebounds up again, gaining
(gravitational) potential energy, reaches the height h, falls, rebounds,
on and on forever. This is great! You do work raising a ball once and, since
energy is conserved, it bounces forever as it converts gravitational energy into
kinetic energy into spring energy (another form of potential energy), back to
kinetic energy, etc. This is a perpetual motion machine! Try it! It won't work.
Why? Because we forgot friction. Eventually the weight will stop bouncing. Well,
there goes conservation of energy. Not quite. Let's just include the frictional
heat as part of the energy. Run another thought experiment: Give a weight a push
across the floor: You push (apply a force) over a distance to get the weight
going (and so do work equal to F
)x)
on the weight. This changes its kinetic energy from zero (the weight was at rest
to begin with) to 1/2 m v2. After a while the weight stops,
as friction opposes its motion and brings it to a stop. What has happened to the
energy? The work done was converted to the heat due to friction. As was argued
by Julius Robert von Meyer, (with some paraphrasing by
me) "If energy, once in existence, cannot be annihilated but only change
its form. what other forms is it capable of assuming?" He then argues
"If work can be converted to heat, then heat must be a form of energy, and
must naturally be equivalent to kinetic and potential energy." The direct
measurement of the "mechanical equivalent of heat" was done by James
Prescott Joule in his famous Paddle Wheel experiment. This continually
expanding role of energy was finally set into comprehensive form by Hermann
Helmholtz who concluded that energy was the sum total of kinetic, potential,
heat, electrical and "other forms to be discovered or invented".
So we have it: Energy has many forms (but only one form of
kinetic energy, 1/2 m v2).
If in our searching we find a process that seems to violate the conservation of
energy, we simply invent another form to take up the slack.
Go to
the previous page