Fluids I

Fluids1

Here we look at the properties of fluids - first static properties, then dynamic properties. A fluid is something that can flow, like a liquid or a gas. Some other things that are fluids are tar (it flows, but slowly) and glass (it flows so slowly that it is usually not thought of as a liquid).

You know that as you go deeper into a pool of water the pressure increases. Question: What is the relation between depth and pressure? To answer this, think of a container (i.e. a lake) holding a fluid (i.e. water). At some depth below the surface you can construct an imaginary disc (or any shape, for that matter) of negligible thickness with surface pointing up^*.

In the picture, an imaginary thin disc of area A sits at the bottom of a water column that extends from the surface down to a depth h.

If the water has density r, the weight of the column is given by mg = rhAg. This downward force (the weight) is balanced by the upward force of the surrounding water on the disc. Since P = F/A the pressure P = rgh. If we add to this the pressure of the atmosphere (P₀), the total pressure at a height h becomes P = rgh + P₀. (The difference between gauge pressure and absolute pressure is the added effect of the atmosphere. You fill your tires according to gauge pressure.)

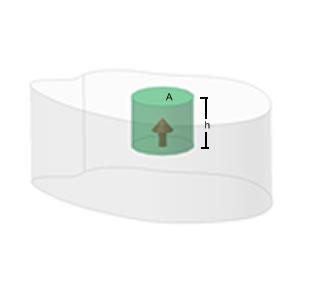Of course, our disc is just a convenient representation of the bottom of a column of water surrounded by more water. As we assume the water doesn't move, every drop of the water must be pushed upon equally (in magnitude and direction) by its surrounding neighbors. Differences in pressure depend only on the depth within the fluid. This is the meaning of Pascal's law: Pressure applied to a container of fluid is distributed equally throughout the container (changing only with depth). That's why, when you fill a teapot, the height of the tea in the pot is the same as it is in the spout. It's also why I didn't need to use the nicely shaped cylinder above - it's just easier to visualize when done this way.

The cylinder I used above was made out of water - the same as the water it was in. Suppose I replaced the water cylinder with one made of lead, or anything more dense than the water. The upward pressure only depends on the depth; that pressure is rghA. But this is just mg, the weight of the water displaced by the cylinder. This upward force is called the buoyant force. The downward force is the weight of the cylinder (now made of lead of mass M) equal to Mg, so the net downward force is that of the lead minus that of the water (or of course, any other fluid). In other words, when an object is immersed in a fluid, it loses as much weight as the weight of the fluid it displaces. This is a statement of Archimedes Principle.

If the object happens to be less dense than water, it sinks just enough to displace its own weight of water. At that point the object has lost all its weight (more formally, the upward (buoyant) and downward (gravitational) forces become equal) and the object floats. Again writing the masses in terms of their densities we have r₀V₀g =r_fV_fg . (The subscripts o and f stand for the object and the fluid). Canceling g and rearranging the terms provides V₀/V_f = r_f / r₀.

So, if the object is for example, 0.92 the density of water (as ice is), then V_f = 0.92 V₀. In other words, the volume of the fluid displaced is 92% of the object's volume so 92% of the ice is under water. (If we are in seawater we use 89% because seawater is a bit denser than fresh water. That's why ships in northern waters worry about icebergs - they're mostly below water and so hard to see.)

^*How can the surface of anything point somewhere? Well, it's just a way of determining the orientation of the surface. Think of a surface in the shape of a wafer, with an arrow pointing up from, and perpendicular to, one side of the wafer. Make this arrow a unit vector and call it the "normal" (i.e. "perpendicular") vector. This will point in the "direction" of the surface. Of course every surface has two possible directions. If the surface is closed for instance, there can be a normal vector pointing out and one pointing in. In this case convention has the positive normal direction outward. For a surface such as ours the choice is arbitrary. For my surface I call upwards the positive direction of the normal vector. The normal vector is shown as the fat arrow in the picture. If the surface is uneven, as in the case of a potato chip, the normal vector varies from place to place, but each spot on the surface still has its own normal (unit) vector.