So far we know the following regarding
The universal law of gravity (and, of course,
(1.1)
Kepler’s three laws (For a synopsis of Kepler’s life look here):
1. Elliptical
orbits
2. Equal areas in equal times
3. T2 = kR3
(And, of course, all the stuff we learned in the first semester).
Kepler formulated his laws by working with data gathered by
Tycho Brahe, famous for constructing large and accurate devices with which to
plot the positions of the planets. Kepler was Tycho’s assistant and, upon
Tycho’s untimely death, he used data on the orbit of Mars to derive his first
two laws. (A review of a book on these two remarkable individuals can be found here). Kepler’s laws
were purely empirical. Early in his work he tried in vain to cast Tycho’s data
into circular form, but finally gave up and let the data speak for itself. The
result was his first two laws. A decade later (1619) he published his third
law. that’s why
The second law: We know that torque ( ) is described as the cross product of moment
arm (r) and force (F),
.
The torque acting on a planet orbiting the Sun is zero, since the force is
directed towards the Sun, as is the radius vector. For circular motion (and all
the planets known to Kepler moved in ellipses that were almost perfect circles
that’s why no one before him thought they were ellipses), the equivalent of
Newton’s second law (written as
) is
.
Since here the torque is zero, it follows that the time rate of change in
angular momentum (L in the equation)
is zero, so the angular momentum of a planet orbiting the Sun doesn’t change
(thankfully
otherwise we wouldn’t be here). Angular
momentum is defined as the cross product of the radius vector and the momentum
of the object,
(1.2)
Look now at the geometry of an orbiting planet, as in the
figure: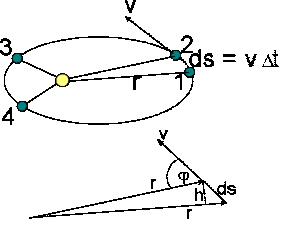 
Shown are the Sun and a planet. The
time it takes to get from 1 to 2 is the same as that from 3 to 4. Because the
planet is closer at 3 and 4, it must move faster in order to sweep out the same
area as when it moves from 1 to 2. But this is exactly how a system conserves
its angular momentum as r
gets smaller, v increases so that
remains constant. Look at this a bit more
formally: Take a very small time interval dt,
and say that in that time the planet moves from 1 to 2, a distance
.
Although this distance is along an arc, for the very small displacement we use here
we can think of it as a straight line (in the limit, it is a straight line). We then have a triangle with base r and height h, and so area
(1.3)
Now divide both sides of (1.3 by dt. This provides
(1.4)
We now need only to multiply both
sides by m (which remains constant) to
recognize that the right-hand side is just the angular momentum of equation (1.2)
with a constant factor of
thrown in. But the angular momentum doesn’t
change! That means
doesn’t change, which is of course, what
Kepler said in his second law. If you have been thinking about this argument
carefully, you might have wondered about my choice of the angle
for the cross product,
and how I can get by labeling two apparently different sun-planet distances with
the same value r. Both are correct
you should be sure you know why.
The third law: This is a consequence of the fact that the force necessary to hold a planet in orbit about the Sun (the centripetal force) is provided by the Sun’s gravity. Setting these two equal we have
(1.5)
where the subscripts assign masses to the Sun and the orbiting planet. The
velocity v of the planet is the
distance it travels in its orbit (2πR) divided by the time it takes to go around (T). Then (1.5) becomes
(1.6) .
Rearranging this gives the result
(1.7) .
The period of the orbit is proportional to the orbital radius cubed. The term is Kepler’s constant. Notice that it contains
the mass of the Sun
that’s why a different constant is required
for each orbiting system.
