Vectors I:

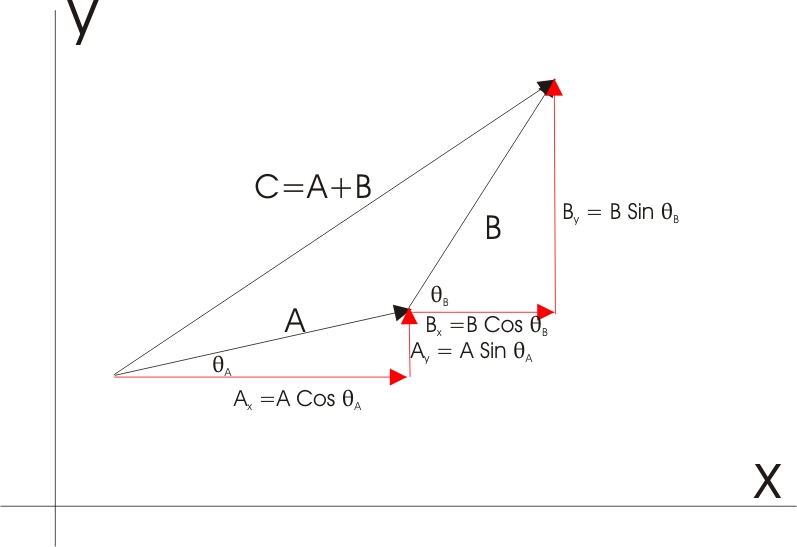
We look at vectors in more detail. An arrow is used to define a particular vector. The length of the arrow represents its magnitude, the orientation of the arrow its direction. All vectors are "free' vectors: They have magnitude and direction, but no preferred location in space.

Start with a right-handed, 3-dimensional coordinate system (I.e. one constructed using the right-hand rule). A vector can be drawn anywhere in this system; for convenience we stick to the x-y plane for now. (The text uses the x-y plane. In class I used the y-z plane. What matters is that in 3-dimensions we, by convention, stick to the right-hand rule). I'll use the x-y plane here.

We say that the vector C is equal to the vector A + the vector B (C = A + B). That means one can be substituted for the other. Question: If we know vectors A and B, how can we find their "resultant", vector C? Answer: Knowing A and B means we know both their magnitudes and their directions (say, as an angle measured up from the x-axis). From this information and the infamous law of cosines (A² + B2 - 2AB Cos 2) can find C. There is however, an easier (and much more useful) way. The method involves the use of right triangles. Right triangles are nice (and other types are bad) because of the following remarkable character of such triangles:

Draw a right triangle - any right triangle - and label one of the angles θ (not the right angle). See the one below.

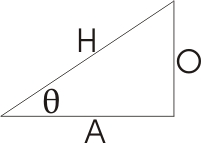
Take the ratios of any two sides, and write them down (e.g. take O/H). Now draw another - any other - right triangle with the same angle θ. Measure the same ratio of sides and you will find that they are the same for both triangles - no matter how big or small the triangle is. This was so remarkable the Greeks named the ratios. The names and the corresponding ratios are:

Sine θ ≡ O/H
Cosine θ ≡ A/H
Tangent θ ≡ O/A

These definitions are the basis for the mathematics of plane trigonometry, and the above mentioned unique property of the ratios should fill you with an overwhelming urge to use right triangles whenever you can, and to try to turn other kinds of triangles into right triangles at every opportunity.

Now go back to the first picture. Since we can replace any vector by others as long as they start and stop at the same places as the original, replace A and B with vectors A_x, A_y and B_x and B_y as shown below. Now we can find C by first finding C_x and C_y, with C_x= A_x + B_x and C_y = A_y + B_y. Since these vectors are parallel with each other, the addition is algebraic rather than vectorial. Having C_x and C_y we can find C using the Pythagorean theorem, and the angle from the x-axis by using the fact that the tangent of that angle is just the ratio of C_y and C_x.