Oscillations 2
A simple
example of SHM is a mass connected to a spring, resting on a smooth (i.e.
frictionless) horizontal surface. The picture shows the important parameters.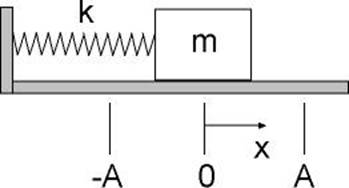
We extend (or compress) the spring
to a maximum amplitude A and let it
go. We want to describe its subsequent motion. Since the force applied to the
block by the spring is given by Hooke’s law ( ), we apply
(1.1)
This is a differential equation (because it involves derivatives – more precisely it carries the impressive title of “second order linear ordinary differential equation with constant coefficients”). We need to solve this by “undoing” the derivatives and so end up with x as a function of time. The usual approach to solving such an equation is to guess the answer. This is not as far-fetched as it may seem, for two reasons: First, to undo the derivatives we must integrate, and that always involves some intuitive guessing; second, it is a characteristic of differential equations that if a solution is found (by any means), it is the only solution. We do have to be sure that, since we must integrate twice, we have the requisite two arbitrary integration constants - a solution with only one would be correct, but not complete. To guide our guesswork, note that we need a solution (x as a function of t) which, when differentiated twice and then added to itself multiplied by is equal to zero. There is only one type of function that meets this requirement – the sine functions (surprise). Try a solution
(1.2)
Differentiate this twice to get
(1.3)
(You should do the differentiation yourself). Substitute (1.2) and (1.3) into (1.1) and cancel the common terms to arrive at the result It seems then, that if we set we have a valid solution and, since both A and f are arbitrary, we have the (complete) solution. Now k and m are fixed when you buy the mass and the spring, so the oscillation frequency is predetermined - w is called the natural frequency (in radians/second) of the system. (More usually we speak of “frequency” (f) in terms of cycles per second – since there are 2p radians in a circle, ).
When we differentiated (1.2) to show that it was the solution to (1.1), we incidentally found the velocity ( ) and acceleration ( ). You should be sure you understand how the position, velocity and acceleration of the block changes as the mass oscillates.
