Waves I

 

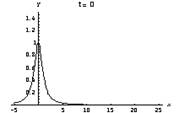
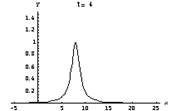
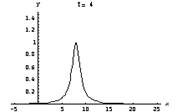
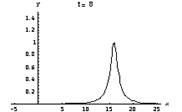
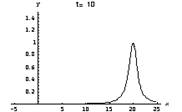
The equation for an object moving in SHM is, as we learned earlier,  (I use y rather than x for the displacement of the object from equilibrium to better match what’s coming, but it’s really the same thing). You should review what each pert of the equation means. We now turn to a discussion of the character of waves. This includes water waves (as in the ocean), sound waves, the wave you get when you pluck a string and, in general, any wave (continuous as in a sine wave or as a single pulse as when you shake a wave into a garden hose). Look first at a long horizontal string (e.g. a string on an infinitely long violin). We pluck the string (or rub it with a bow). How can we describe the resulting pulse that travels down the string? Say you pluck it at time 0 and at the point x = 0. Below is a picture of what results – the pulse moves along the string and, if there is no energy lost in the process, the shape of the pulse will remain unchanged. In case it’s too hard to see, the vertical axis is the displacement of the string (y) and the horizontal axis is the position along the string (x). Each box is a snapshot of the pulse showing where it is at 2 second intervals starting at t = 0.

 

 

An animation of the above pattern looks like this:

 

How do you describe such a wave (a wave is just a pulse – or a sequence of pulses – that moves). Suppose the wave moves with velocity v. Then at some time t after the pulse was created at x = 0 and t = 0 it will be a distance  along the string. But it will look the same (i.e. have the same shape) as it did initially. The amplitude of the pulse changes as x does and its location (x) depends on time – in other words  Since the geometry of the pulse remains unchanged it must be that in general  This general form assures us that no matter what time we insert, the wave looks exactly as it did a distance back at the beginning. (Try it – if the pulse moves with velocity 4 (in any appropriate units), at a time 6 after it starts the pulse is at x = 24 and we have  ) – it works!  And it works for any function of  (For the sketches above I used  with v = 2). OK, this is fine for a single pulse – what about a continuous stream of (repeating) pulses? Well, there’s in infinite variety of pulse streams you can think of, but recall that virtually any periodic wave shape can be represented as a series of sine and cosine waves (Fourier’s theorem), so all we need to look at are sine waves. We write our general equation as

(1.1)

 

 

 This meets our requirement for a function involving  The constant k is included to make the argument of the sine function dimensionless – it must have units of 1/length – and to provide a characteristic property of the wave, namely that it repeat itself once every cycle of the sine function. The value of k that does the job is  Here  is the wavelength of the wave so every time x is an integer multiple of  the wave completes a full cycle (for any fixed value of t). A few more steps will cast our wave into a more standard form: Rewrite (1.1) as  and note that the wavelength is related to the velocity of the wave and its period by  Then  and we have

(1.2)

 

Here  is the angular frequency of the wave and k is called the wave number. They carry the temporal and spatial information about the wave. Keep in mind that the wave moves down the string – it carries energy and momentum (and in the case of sound and electromagnetic waves, information). The string itself only moves up and down. An interesting animation of a traveling wave can be seen here.