Frames of Reference - Einstein's Special Theory of Relativity
Back to the main page/Back to the previous page

The Galilean transformations make eminent sense - they explain our every day motions in a clear and unambiguous way. We attach ourselves and our instruments to a convenient reference frame and conduct our experiments. If another observer looks in from another inertial frame, our work is easily reconciled with this simple transformation. Newton allowed that there may be an absolute reference frame to which all motions could be traced, but knew that using such a frame gave no advantage over any other, as Galileo stated before him. This state of affairs took an interesting turn thanks to the work of James Clerk Maxwell (1831 - 1879) who unified the fields of electricity and magnetism and established that ordinary light was a manifestation of combined electric and magnetic waves. An inconsistency between Maxwell's theory and the transformations of Galileo and Newton led Albert Einstein to propose his Special Theory of Relativity. This theory may be stated in terms of two postulates: 1. The laws of physics are the same in any inertial frame, and 2. The velocity of light is the same for all observers, regardless of their relative motions. The first postulate is a reaffirmation of Galilean relativity; the second imposes a new and unique character to light. Unlike the ball being tossed by Dick and Spot, if instead they fired light beams at each other, the second postulate requires that Dick, Spot and Jane all see the light beam move with the same velocity. (A proper understanding of the implications of these postulates requires a historical perspective).

See Jane watch Dick and Spot play ball. Look again at the situation of Dick and Jane as he rides past her at constant velocity v. To make the situation a bit more believable (and historical - moving trains were a favorite of Einstein), replace Dick's wagon with a railroad flat car, so that he has a bit more space in which to experiment. Consider Dick and that remarkable dog Spot having a game of catch. Dick, in his primed frame, throws the ball to Spot with velocity u'. Jane, from her place on the ground, sees the ball move with velocity u = u' + v. (See Note 1 If this does not seem obvious). This is a simple and every-day application of the Galilean transformation - we add the velocities of the ball and the train to accomplish the transformation. Using some numbers, suppose the train moves at v = 20 m/s and Dick throws the ball at 5 m/s. Then Jane sees the ball moving at 5 + 20 = 25 m/s, as our experience affirms. Suppose now that we somehow slow light down to a speed of 5 m/s (to see how physicists have slowed light down to comparable speeds, click here). In this situation, Einstein's second postulate states that the light as seen by Jane remains at 5 m/s., in contradiction to the requirements of the Galilean transformation.

You should check the links above for a better insight into Einstein's work. His two postulates lead to results that seem strange indeed, but they are unavoidable: To observers moving relative to each other at constant speeds, lengths contract, time dilates, mass increases and mass is just so much energy. It's easy to say that these things occur, but how do we actually know, and how did Einstein find out? The key to Einstein's understanding is in his concept of simultaneity, i.e. his answer to the question: Are 'simultaneous' events really simultaneous when viewed from different reference frames? In Galilean relativity, and in all that Newton did, time was taken to be absolute. In Newton's words, "Absolute, true and mathematical time, of itself and from its own nature, flows equally and without relation to anything external..." Einstein took exception to this: observers in relative motion cannot say they observe a particular event simultaneously. It's time to call on Dick and Jane again (Spot takes a well deserved rest).

See Dick on the flatcar. Dick stands on the flatcar exactly half way between the two bulbs, which are caused to flash. The clocks near the bulbs record the events. If dick sees the two simultaneously, he says that t1 (the time it takes for left flash to reach him) is equal to t2 (the time it takes for right flash to reach him), because he knows how fast light travels, and both distances are the same. Of course, if the flatcar happens to be moving to the right with velocity v, this is of no consequence, because Dick is still on an inertial frame, at rest with respect to the clocks.

See Jane watch Dick. Jane, with her own set of clocks fixed in her frame (not shown), has a different result. She sees the light from the right hand bulb arrive at Dick in a time t2 that is less than t1, because from her frame, Dick moves toward the right hand light beam and away from the left hand one, making the two distances different. In her reference frame the events are not simultaneous. According to this, we can no longer take times in one frame to be the same as times in another.

This lack of simultaneity leads to the changes in time, mass and length mentioned above, and to the famous equation e = mc². To see how these results come about, we can proceed in the following way:

For the record, lets restate our two guiding principles, as postulated by Einstein:

    Physical laws are invariant from one inertial frame to another.

    The velocity of light is constant, regardless of the motion of the observer.

The Galilean transformation equations are

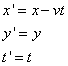
as was stated earlier. These equations assumed that time was the same for both Dick and Jane, even when they were in relative motion, and that events in one frame could be reconciled to the other by the simple additions of velocities. Now Einstein's second postulate requires that we abandon the rule of addition of velocities. The Galilean transformations must be modified. As the historical perspective described, Lorentz and FitzGerald, using the results of the Michelson-Morley experiment, found the required transformation. (Click here for a brief look at how the transformation can be derived). Central to the modified transformation is the "relativistic factor" g. This factor is of the form

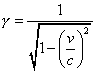
as the historical perspective described. Recall that g is very nearly 1 for velocities common to us all, and becomes appreciably larger than 1 only for very high velocities, approaching the velocity of light. An immediate consequence of the modified transformation is to affect length, time and mass, all through the effect of g on these quantities. The modifications take the form

.

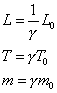Let's see what these mean: Remember, read equations like stories. In each of these equations the subscript ₀ means that the quantity is taken to be measured in the rest frame, thus L₀ is the length of an object, say a meter stick, which is at rest, T₀ is a time interval as measured in a reference frame at rest, and m₀ is the mass of an object, again in a system at rest. The quantities L, T and m are the length, time interval and mass of these same objects, but have the values as measured by an observer moving with some velocity v  relative to the rest system. The velocity v appears imbedded in g, along with c, the velocity of light. The ratio of v to c is the critical quantity: As v gets large and approaches c, the square of this ratio approaches 1 and makes the denominator of g get small, and so g becomes large, approaching infinity as v gets very close to c. The results are now obvious from the equations, if not from your intuition: Lengths contract, time stretches out (dilates), and mass increases. Again, let's use a numerical example: Suppose Jane roars past Dick in her rocket ship, traveling at a speed of 80% that of light - i.e. v = 0.8c. Then v/c = 0.8 and (v/c)² = 0.64. This makes 1 - (v/c)² = 0.36. The square root of 0.36 = 0.6 and so g = 1/0.6 or 1.67. To Jane, everything in her rocket ship is the same as when she was back on Earth with Dick. Dick, however, as he monitors Jane's ship with his instruments, sees things quite differently. A meter stick in the rocket ship has a length as measured by Dick to be 0.6 meters long (the stick is aligned along the direction of the ship's motion). As Dick monitors Jane's pulse rate it is slower, with the time between beats of her heart 1.67 times longer than normal. Finally, as Dick measures Jane's mass it is 1.67 times more than the value measured at rest.

Are these effects real, or just theory? The fact of the matter is that they are real indeed. How do we know? No one has moved as Jane has in the above example. There are, however, things that routinely travel at speeds close to that of light. A classic example is that of the : (the Greek letter mu) meson. These particles are constantly bombarding Earth, arriving at velocities of 0.998 c. Laboratory experiments show that these mesons have a lifetime of about 2 X 10^-6 seconds. The distance a meson can cover before decaying is then 0.998 x 3 X 10⁸ m/s x 2 X 10^-6 s, or about 600 meters (recall that the velocity of light, c = 3 X 10⁸ m/s), Thus, neglecting relativistic effects, : mesons can reach the earth if they are created at a height of 600 meters or less. We know that these particles are created at heights at least 10 times higher, over 6000 meters. How then can they ever reach Earth? At these speeds we need to invoke special relativity. From the : meson's perspective, its lifetime of 2 X 10^-6 seconds is unchanged, but the distance to Earth is contracted. At its velocity g becomes 15.8, and using the first of the equations above, the distance of 6000 meters contracts to a meager 380 meters, a short trip for the meson. What about observers on Earth? For them the distance is still 6000 meters, but the time available increases. g is still 15.8, and so, from the third equation, the time available for the meson's flight is dilated from 2 X 10^-6 seconds to 31.6 X 10^-6 seconds - plenty of time to cover the required distance. Relativistic calculations are routine in laboratories, and the above relations are confirmed every day. The theory of special relativity is firmly established as part of the basic laws of Nature.

 One further comment on special relativity: Although light waves have no mass, relativistic calculations predict they possess momentum and relativistic energy. When this concept is followed, the result is a relationship between energy and mass, given be the famous E = mc². While the mathematics leading to this result is a bit more involved than that leading to the above transformations, it still involves only algebra and is part of most introductory physics courses. You may want to look at reference 2 for more details.

Back to the top.
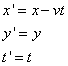
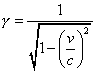
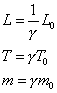