The behavior of gasses:
Matter exists in three states - solid,
liquid and gaseous. Of the three the third is the less complex. The molecules
that make up the gas move independently of each other except as is occasioned by
collisions with each other or the walls of their container. In keeping with our
tendency to look at problems that best lend themselves to analysis we look at
the properties of gasses. A gas can be characterized by three parameters - the
volume of the container that holds it; the pressure it is subjected to; the
temperature it is held at.
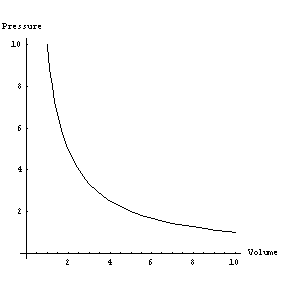 Experiments
by Boyle and Mariotte in the 17th century led to an empirical relation known as
Boyle's law: If the temperature of a gas is held constant, the product of its
pressure and its volume remain constant. As an equation, p
V = Kt, Kt being a constant whose value
depends on the amount of gas involved - i.e. its mass. The subscript t
is a reminder that the temperature is held constant during the experiment. A
graph of pressure vs. volume is shown on the right, using arbitrary units. Note
for example that when V
equals 2 the pressure is 5 and when V equals 5 the pressure is 2 - for this
situation the constant is 10.
Experiments
by Boyle and Mariotte in the 17th century led to an empirical relation known as
Boyle's law: If the temperature of a gas is held constant, the product of its
pressure and its volume remain constant. As an equation, p
V = Kt, Kt being a constant whose value
depends on the amount of gas involved - i.e. its mass. The subscript t
is a reminder that the temperature is held constant during the experiment. A
graph of pressure vs. volume is shown on the right, using arbitrary units. Note
for example that when V
equals 2 the pressure is 5 and when V equals 5 the pressure is 2 - for this
situation the constant is 10.
Almost a century after these
experiments were reported Jacques Charles and Joseph Gay-Lussac
independently experimented with gasses held at constant pressure. Their
temperature-volume relation is V = Kp T, where the
constant Kp here is different from that of Boyle's
experiments, but still depends on the mass of gas used. This empirical
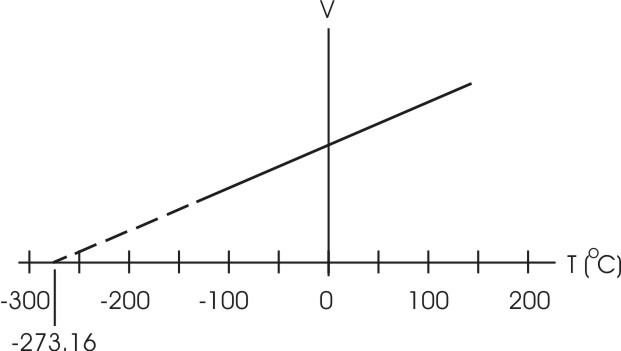
result is known as Charles' law. This is also plotted on the right. Note
that in the extreme case of zero volume the temperature goes to -273.16
degrees C. The dotted portion of the line indicates an extrapolation from
measurable results. As a volume cannot be less than zero the number
-273.16 is an absolute zero value for temperature.
We can combine these two "laws"
into one by writing p V = K T. In this form, if T is
held constant then KT becomes our earlier constant Kt,
and if the pressure is held constant we replace K/p with Kp.
We may also hold the volume constant and show that temperature and
pressure are related by p = KV T in keeping with our
combined form. An important result occurs if the gas
concentration is kept low: In this case these relations hold regardless of what gas is
used. A gas dilute enough to loose its identity while conducting
these experiments is called an ideal gas. Also, if the experiments are conducted on equal volumes of gas instead
of on equal masses, the value of K is independent of which
gas is used.
This ideal gas
law, p V = K T, came from the empirical evidence of many
experiments. What underlying structure exists to bring it about? Such a
structure should explain the equation and why it is most general for low
gas densities and equal masses. Boyle had supported the idea that gasses
were made of discrete corpuscles. As the great success of Newton's
mechanics strongly influenced physicists of the time, it was natural that
a mechanical model was pursued.
 We start with the assumption that gasses
are made of accumulations of molecules, and in the simplest case these can be
considered to be points of mass. These molecules move about in their containers
in a random manner - the degree of their motion (i.e. their velocity or kinetic
energy) depending on the state of the gas. We study their motion by
applying Newton's laws of motion. In doing so we deduce that when these
molecules collide with each other or the walls of their containers the
collisions are perfectly elastic (otherwise the resultant energy loss would
eventually cause the molecular motion to stop). By designing our molecules to be
points of mass we introduce two important simplifications: As point masses they
occupy essentially zero volume and so 1) cannot collide with each other; 2) do
not occupy any of the volume of the container. These two simplifications become
more realistic as the densities of the gasses decrease - i.e. as the gas becomes
"ideal".
We start with the assumption that gasses
are made of accumulations of molecules, and in the simplest case these can be
considered to be points of mass. These molecules move about in their containers
in a random manner - the degree of their motion (i.e. their velocity or kinetic
energy) depending on the state of the gas. We study their motion by
applying Newton's laws of motion. In doing so we deduce that when these
molecules collide with each other or the walls of their containers the
collisions are perfectly elastic (otherwise the resultant energy loss would
eventually cause the molecular motion to stop). By designing our molecules to be
points of mass we introduce two important simplifications: As point masses they
occupy essentially zero volume and so 1) cannot collide with each other; 2) do
not occupy any of the volume of the container. These two simplifications become
more realistic as the densities of the gasses decrease - i.e. as the gas becomes
"ideal".
With this model we proceed as follows:
Take
a single molecule of our ideal gas. As one of a large number (N) of such
molecules we may assume its velocity is the average velocity of all the
molecules in the gas. In general the molecules move randomly in space, so one
would expect that at any time 1/3 of them would be moving in each of the three
available directions x, y and z. (If this doesn't sit well with you, note that
if an average molecule were moving in any random direction it's components
along the perpendicular directions would be equally distributed). Say our
molecule is moving in the x-direction with velocity vx. When
it hits the right wall it will rebound with a momentum change dp = 2mvx,
and will do so again after rebounding off of the left wall. The total round trip
covers a distance 2L so the time it takes for a round trip is dt = 2L /vx
seconds. This means there is a force of (since Newton's second law
says
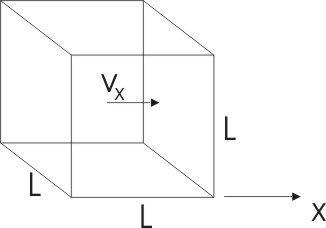 F = dp/dt)
F = dp/dt)
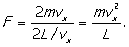
Now pressure (p) is force per unit
area and for our cube of sides L the area of a face is L2,
so we may write this force as pL2. This leads to a pressure on
the wall (due to our single molecule) of
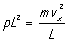
(Now we use p for pressure
rather than momentum - there's just not enough letters to go around - but the
context should keep things clear.)
Our gas consists of N molecules,
and
1/3 of these will be moving in the x-direction, contributing to the total pressure
on the wall N/3 times that of our single molecule. Recognizing that L3 is just the
volume of the gas (which we move to the left side) and after inserting a factor
of 2/2 in to bring a familiar friend to the fore) we have
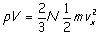
Conclusion: The pressure times the volume of the gas
equals two thirds the number of molecules times the average kinetic energy of a
molecule of the gas. (Or, dividing by V shows that the pressure is just the average
kinetic energy of a molecule times the number of molecules per unit volume -
times the factor of 2/3 - where does this pesky 2/3 come from?).
The pressure of a gas is the result of
collisions of air molecules with the sides of the container - the more energetic
the molecules, the greater the pressure.
We need to match our derived equation to the experimentally
arrived at ideal gas law (p V = K T). Recall that K (the
"gas constant") was a constant independent of the type, but tied to
the volume of the gas. The connection comes from a theory by the Italian
physicist Amedeo Avogadro that equal volumes of gasses contain equal numbers of
molecules. This being so, K must be proportional to N and we may
write K = k N where our new constant k is the gas constant
per molecule, known as Boltzmann's constant. Using this and equating the
right hand side of the ideal gas law to the right hand side of the results of
our model yields
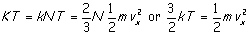
and the ideal gas law becomes (now
referring to a gas with N molecules)
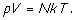
The end result is the gratifying
conclusion that completely supports the (at the time controversial) molecular
nature of gasses, arrived at by a purely mechanical application of Newton's
laws. It also
clearly shows that temperature is a result of molecular motion, contained in the
kinetic energy of the moving molecules. Since kinetic energy cannot be negative
it follows that if the molecules of a gas somehow can slow down and come to
rest, the resulting temperature must reach a minimum attainable value of zero.
The temperature in the gas law is an absolute reference to the energy of the gas
- its absolute temperature T. This is the limiting value of the graph of V
vs. T experimentally arrived at by Charles and Gay-Lussac.
As an example of the consequences of
these relations, from
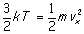
it follows that the average velocity
(more properly, speed) of a
gas molecule is
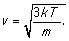
Boltzmann's constant has the value k
= 1.38x10-23 , room temperature is about 300 K. A Nitrogen molecule
(of which air is mostly made) has an atomic weight of 14 AMU (atomic mass
units), and 1 AMU = 1.66x10-27 kg. Inserting these into the velocity
formula provides v = 730 m/sec. This is about as fast as a bullet from a high
powered rifle.
stats
 We start with the assumption that gasses
are made of accumulations of molecules, and in the simplest case these can be
considered to be points of mass. These molecules move about in their containers
in a random manner - the degree of their motion (i.e. their velocity or kinetic
energy) depending on the state of the gas. We study their motion by
applying Newton's laws of motion. In doing so we deduce that when these
molecules collide with each other or the walls of their containers the
collisions are perfectly elastic (otherwise the resultant energy loss would
eventually cause the molecular motion to stop). By designing our molecules to be
points of mass we introduce two important simplifications: As point masses they
occupy essentially zero volume and so 1) cannot collide with each other; 2) do
not occupy any of the volume of the container. These two simplifications become
more realistic as the densities of the gasses decrease - i.e. as the gas becomes
"ideal".
We start with the assumption that gasses
are made of accumulations of molecules, and in the simplest case these can be
considered to be points of mass. These molecules move about in their containers
in a random manner - the degree of their motion (i.e. their velocity or kinetic
energy) depending on the state of the gas. We study their motion by
applying Newton's laws of motion. In doing so we deduce that when these
molecules collide with each other or the walls of their containers the
collisions are perfectly elastic (otherwise the resultant energy loss would
eventually cause the molecular motion to stop). By designing our molecules to be
points of mass we introduce two important simplifications: As point masses they
occupy essentially zero volume and so 1) cannot collide with each other; 2) do
not occupy any of the volume of the container. These two simplifications become
more realistic as the densities of the gasses decrease - i.e. as the gas becomes
"ideal". Experiments
by Boyle and Mariotte in the 17th century led to an empirical relation known as
Boyle's law: If the temperature of a gas is held constant, the product of its
pressure and its volume remain constant. As an equation, p
V = Kt, Kt being a constant whose value
depends on the amount of gas involved - i.e. its mass. The subscript t
is a reminder that the temperature is held constant during the experiment. A
graph of pressure vs. volume is shown on the right, using arbitrary units. Note
for example that when V
equals 2 the pressure is 5 and when V equals 5 the pressure is 2 - for this
situation the constant is 10.
Experiments
by Boyle and Mariotte in the 17th century led to an empirical relation known as
Boyle's law: If the temperature of a gas is held constant, the product of its
pressure and its volume remain constant. As an equation, p
V = Kt, Kt being a constant whose value
depends on the amount of gas involved - i.e. its mass. The subscript t
is a reminder that the temperature is held constant during the experiment. A
graph of pressure vs. volume is shown on the right, using arbitrary units. Note
for example that when V
equals 2 the pressure is 5 and when V equals 5 the pressure is 2 - for this
situation the constant is 10.
 F = dp/dt)
F = dp/dt)