Basic Ideas about Motion
Go back to the previous page.
Go back to the home page.
We need to be able to describe the motion
of things (for obvious reasons). To be coherent in a discussion of motion, we
first must agree on a common vocabulary, so I show here a glossary of terms we
will use:
Speed:
How fast our object is moving.
Velocity: How fast (or more
formally, the rate at which) our object is moving, and the direction in
which it is moving.
(Already, we have come upon an important distinction - speed
can be described by a number, say 20 m/s, but for velocity we require more.
We take the velocity of our object to be its speed combined
with the direction of its motion. This distinction is generalized into the
mathematical ideas of scalars and vectors, which we define next).
Scalars:
A scalar is something whose measure is defined
by its magnitude. Examples are speed (how fast), temperature (how hot), length
(how long), and many more. (Think of a few).
Vectors:
Vectors require direction as well as magnitude
to describe their measure. Examples are velocity (speed, and the direction of
the motion; 20 m/s to the northeast), Force (how hard you push, and in what
direction - to convince yourself that force is a vector rather than a scalar,
try pushing on something without pushing in a particular direction). There are many
more. (Again, try to think of some).
Now we can get back to motion:
Acceleration: The rate at which velocity changes. Now we may be getting
into new territory. Not that you haven't heard of acceleration, but have you really thought
about it? You drive along at 40 miles per hour. Your speed is constant and
you are on a straight section of road , your direction and speed - and so your velocity
- does not change. Your acceleration is zero, right? Sure it is. Now you step on
the gas, and you accelerate - you go faster. How much faster? If for every
second you keep accelerating your velocity increases by, say, 2 miles per hour,
your acceleration is 2 miles per hour per second. Using more consistent
(if less familiar) units, lets say you accelerate at a rate of 2 meters per
second every second. Your acceleration is 2 m/s per sec, or 2 m/s2.
(Click here for a discussion of dimensional consistency.)
Position: Where our object is, relative to some reference frame. The reference frame
defines the origin of our coordinate system, from which all measurements are
made.
With these definitions we can describe
the motion of an object. By an object I mean a simple particle, consisting of a
single point in space. It can also be a point representing an object whose size
makes its extent negligible compared to the rest of the system under
consideration. For example, a baseball is essentially a point compared to a
baseball stadium, as is the earth compared to the solar system.
First we establish our
coordinate system.
We choose a rectilinear, orthogonal system (i.e. a Cartesian system) with origin
at (0,0,0). Using this coordinate system we can quantitatively discuss the
motion of our object. Motions, of course, can be very complex - so complex
in fact, that a head-on approach to analysis can be daunting. The trick
that scientists continually play is to break complex things down into
simple things, and then work on those. Once the simple components of our
complex problem are understood, we join the solutions to finally
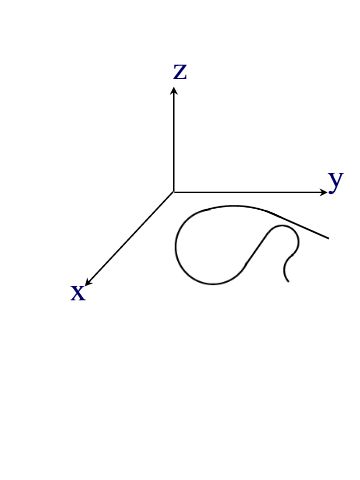
understand the initial problem. Here's a case in point: The picture shows
the motion of an ant as it walks on a table. (A fly buzzing around the
room would be the three-dimensional analogy). The motion is complex, but
think about it: things move
in straight lines or they curve. But any curve, at least over a small
enough part if it, can be thought of as part of a circle. Click on the
curve to the right and see what I mean. If we address small parts at a
time, the complicated path of the ant becomes simple, and we can build up
an understandable (i.e. quantitatively describable) picture of its motion.
Once we simplify the motion into
straight lines and circles, we further break down the straight line motion
into its x-, y- and z-components, and the circular motion into rotation
about the center of the circle. We will look at the mechanics of doing
this later.
|
|
Go to
Newton's laws of motion
